
No importa el tipo de economía de que se trate, el dinero tiene una función relativa al tiempo. Es decir, el dinero siempre es menos valioso que el pasado y más valioso que a futuro, esto, aunque no exista inflación.
Lo anterior se da por la interacción de todos los valores que el dinero representa, siendo básicamente:
Una unidad de cambio
Un atesoramiento de riqueza
De acuerdo a lo anterior podemos analizar que si una persona renuncia a gastar un dinero suyo y prestarlo o darlo en custodia, merece recibir un determinado premio por diferir su beneficio presente, comúnmente llamado interés.
Interés Simple
Es el premio por diferir nuestro gasto en un período de tiempo.
La fórmula para calcular el interés simple es:
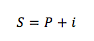
Siendo:
P=Cantidad de dinero en el presente
i=Interés Ganado
S=Valor Final
Para determinar los intereses del período multiplicamos la cantidad por la tasa de interés:
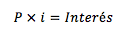
Recuerde que P es el dinero original, i es la tasa que se pagará. Regresando a nuestra fórmula de interés simple, sustituimos los intereses por su cálculo:
S=P+(P×i)
Supongamos que nuestro capital es de 100 y la tasa de interés es de 9%:
S=100+(100 × .09)
S=100+(100 × .09)
S=100+(9)
S=109
Otra forma de representar la fórmula de interés simple, pero es exactamente igual es:
S=P × (1+i)
En nuestro ejemplo sería:
S=100 × (1+.09)
S=100 × (1.09)
S=109
Interés Compuesto
Cuando los períodos de inversión se repiten y se ganan nuevos intereses sobre los intereses del primer período, se le llama interés compuesto.
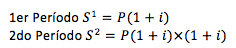
o bien
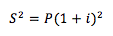
No importa el número de período en que se repita, mientras sea el mismo interés y los mismos períodos podremos usar la expresión:
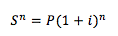
Para nuestro ejemplo de 100 como capital, 9% de intereses y 5 períodos, sería:
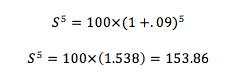
Hacer estos cálculos sin la fórmula general sería muy largo y si los períodos fueran muchos sería casi imposible, en nuestro ejemplo, si lo hubiéramos hecho con la fórmula del interés simple sería así:
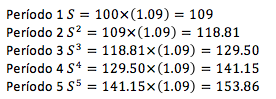
Entonces, el Interés Compuesto es el interés acumulado que gana una inversión fija en varios períodos iguales de tiempo.
Valor Actual
Pero supongamos que es al revés, que lo que necesitamos saber no es el valor del dinero en el futuro, sino que sabiendo el valor futuro, quisiéramos saber su equivalencia en el presente, es decir, saber cuanto dinero debemos invertir en el presente a una tasa determinada, con interés compuesto, para que se convierta en la cantidad deseada o sabida en el futuro.
Supongamos que queremos 10,000 en 5 años y, nos ofrecen 20% anual sobre nuestra inversión, la pregunta es: ¿Cuánto dinero debo invertir hoy para que se convierta en 10,000 en 5 años con interés compuesto, con una tasa de 20% anual?
Utilizando la fórmula general de interés compuesto:
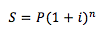
Sustituyendo en nuestro ejemplo, los valores del ejemplo:
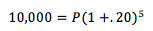
Despejando P, valor actual, tenemos:
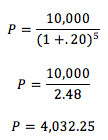
Debemos invertir 4,032.25 hoy para que se conviertan en 10, 000 en 5 años con una tasa de 20%. La fórmula general de valor presente será:
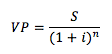
Donde:
VP= Valor presente
S= Valor futuro
i= Tasa de interés
n= Número de períodos
Si acaso encuentran otra expresión de VP como:
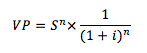
Es exactamente lo mismo.
Una aclaración que confunde mucho, por ejemplo, cuando nos dan una tasa anual pero nos indica que se capitaliza trimestralmente. Debemos hacer equivalente los períodos a la tasa, es decir, por un lado debemos dividir la tasa (anual) entre los trimestres del año que son 4. Y por otro lado debemos multiplicar los períodos también por 4.
Donde:
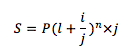
J significa los períodos de capitalización dentro de un año cuando la tasa es anual.
Ejemplos:
Interés compuesto.
Queremos saber el valor futuro (S) de una inversión presente de 1, 000 a 7 años con una tasa de 10% capitalizable cada mes:
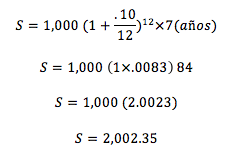
Con el mismo ejemplo pero para Valor Actual (VA):
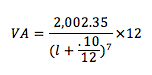
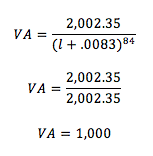
Resultará de lo más importante, para efectos de análisis, tomar en cuenta siempre el valor presente del dinero o su valor futuro, dada una tasa de interés para poder comparar el valor del dinero equivalente, ya dijimos desde el principio que el dinero no es igual en función al tiempo, y no tiene que ver con la inflación o con una tasa bancaria, es tan simple como la percepción de la diferencia entre gastar mi dinero hoy o guardarlo 5 años para gastarlo, la tasa de interés para calcular puede ser el interés que me de un banco o puede ser la ganancia que espero en un negocio al que meto mi dinero hoy.
Cualquier decisión que se tome con respecto al dinero en función del tiempo, será hecha con valores equivalentes en ese mismo tiempo.
Siguiendo con el tema, supongamos que se tiene el valor actual, el valor futuro y los períodos, pero no se sabe la tasa de interés, partimos de:
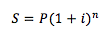
Y despejamos :
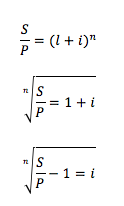
Tomando los datos del ejemplo anterior:
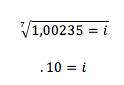
Hugo Villanueva Cantón
www.toka.com.mx
EXCELENTE AMIGO
Escribe tu comentario |